coniques

D'un point de vue algébrique, une pCourbe se présente sous la forme d'un polynome dont les coefficients sont des points :

un segment contrôlé par deux points : P = (1-t^2).p0 + t^2.p1, avec t dans [0,1]
une parabole contrôlée par trois points : P = (1-t^3).p0 + (1-t^2).t.p1 + (1-t).t^2.p2 + t^3.p3
etc ...

On démontre que l'équation d'un cercle (x = r.cos(a) et y=r.sin(a), avec a dans [0,2.pi]), est irréductible à la forme polynomiale ; par un changement de variable (t=tan(a/2)) on peut au mieux la réduire au quotient de deux polynomes, dite forme "rationnelle" : x = (1-t^2)/(1+t^2), y = (2t)/(1+t^2), , avec t dans [-infini,+infini]. Il est donc a priori impossible de représenter un cercle avec les formes pascaliennes ! Par bonheur les grecs ont découvert les coniques : un cercle, une ellipse, une parabole, une hyperbole sont des courbes apparemment très différentes, si elles sont envisagées dans le plan. Considérées dans l'espace, elles peuvent être vues comme simples intersections entre un plan et un cône à base circulaire et c'est l'inclinaison du plan sur l'axe du cône qui fait les différences.

Le premier résultat est que chacune de ces courbes peut être vue comme projection de n'importe quelle autre depuis le sommet, et notamment le cercle comme projection de la parabole. L'ombre sur un plan d'une parabole tracée dans l'espace est un arc de cercle, à supposer que la source lumineuse ait été bien placée. L'intérêt ? Eh bien la plus simple des courbes pascaliennes, après la ligne droite, est une parabole ; on sait donc tracer des cercles sur un plan (espace bidimensionnel) à partir d'une parabole dans l'espace tridimensionnel, et en montant d'une dimension, on sait tracer des cercles dans notre espace tridimensionnel à partir de paraboles définies dans un espace quadridimensionnel. Peu importe qu'il soit difficile de visualiser un tel espace, on ne s'intéresse qu'à son ombre !

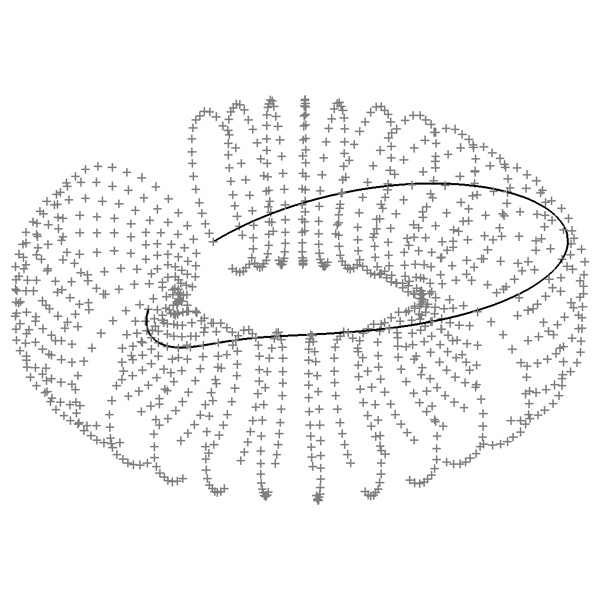
La porte est donc ouverte à la construction de cercles, puis de cylindres, de sphères, de tores, de toutes les formes de révolution. L'exemple présenté ici montre un tore presque complet sur lequel est tracé ... un cercle presque complet. Et c'est là l'un des intérêts de définir un cercle à partir d'une parabole (et pas à partir d'un simple compas) : la possibilité d'étendre la construction du cercle et des formes qu'il peut engendrer à des espaces courbes (comme la surface du tore). Un autre intérêt non négligeable est qu'il est possible d'oublier définitivement les fonctions trigonométriques (sinus, cosinus,...), simples leures cachant une transcendance inaccessible (ouaaaaaouhh!) ; définir un cercle par x = r.cos(a) et y=r.sin(a) semble anodin et est en fait terriblement frustrant, on fait appel à des fonctions transcendantes qui ont longtemps été consignées dans ce qu'on appelait les tables trigonométriques, pour finir hard-codées dans nos calculettes et ordinateurs.

images

La première image représente un segment immergé dans un tore (presque fermé) ; le tore est une simple pS33, on démontre que le segment est une pCourbe à (3+3-2)(2-1)+1 = 5 points de contrôle.
La seconde image représente un flacon, une surface de révolution construite sur une pCourbe contrôlée par 7 points, immergé dans un cube de contrôle dont les points sont déplacés en rotation, avec comme effet une déformation globale du flacon
La troisième image représente un cercle immergé dans un tore. Voici le code produisant la dernière image représentant un cercle immergé dans un tore :

def cercle_in_tore( r1=0.5, r2=0.2, r=0.3, avec_tore=true )
	section = Cercle.new( r2 )           # demi-cercle r2 sur l'origine
	section.translate( [r1,0,0] )        # translation de r1
	profil = Cercle.new( 1.0 )           # cercle unitaire
	pTore = Cross.new( profil, section ) # quart de tore [0°,0°]-[180°,180°]
	pTore.rotate( [90,0,0] )             # pivoté sur Ox
	pTore.complet()                      # ... tore complet [-90°,90°]-[270°,270°]
	if (avec_tore)                       # affichage conditionnel du tore
		pTore.build( 3 )
		pTore.draw( "S" )
	end
	pCercle = Cercle.new( r )            # arc de cercle 180°, rayon r
	pCercle.translate( [0.5,0.5,0.0] )   # défini en local sur le tore
	pCercle.complet()                    # cercle complet sur 360°
	tab = pCercle.build( 5 )             # tableau issu de la subdivision
	tab.each_index do |i|
		tab[i] = pTore.get_point( tab[i] )  # passage en global
	end
	pf = PF.new( tab )
		pf.draw( "L" )               # déjà subdivisé avant local -> global
end

diverses autres choses

à suivre ...