conics

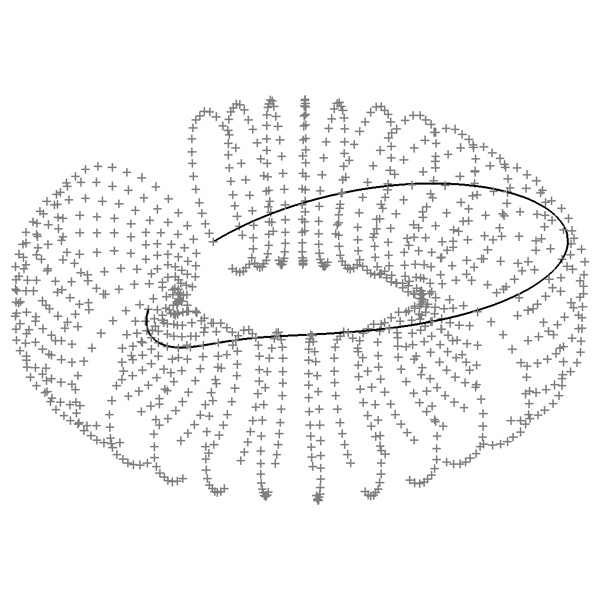
It would be thus impossible to represent… a circle with pascalian forms. Fortunately Greeks discovered conics: a circle, an ellipse, a parabola, an hyperbolae are apparently very different curves, if they are envisaged in the plan. Considered in the space, they can be seen as simple intersections between a plan and a cone with circular base; it is the slope of the plan on the axis of the cone that makes the differences.

The first consequence of this kind of curves’ description is that each of them can be seen as a projection of any other one from the summit of the cone, in particular the circle as projection of the parabola: the shadow on a plan of a parabola drawn in the space is an arc of a circle, supposing that the light source is placed well. What is the interest in all this? The simplest of pascalian curves, after the straight line, is a parabola! The door is thus open for the construction of circles, then of cylinders, spheres, torus and of all the forms of revolution. The example presented here shows an almost complete tore on which is drawn… an almost complete circle. Here is one of the interests of defining a circle from a parabola (and not from a simple compass): the possibility of widening the construction of the circle and of the forms he can engender in curved spaces (as the surface of the tore). Another not unimportant interest is that it is possible to forget definitively the trigonometric functions (sine, cosine), simple illusion hiding an inaccessible transcendence (ouaaaaaouhh). To define a circle by x = r.cos (a) and y=r.sin (a) seems harmless and is in fact terribly frustrating! We call for transcendental functions which were deposited for a long time in what we call trigonometric tables, to finish hard - coded in our pocket calculators and computers.

Here is the code producing the last image representing a circle immersed in a torus:

def cercle_in_tore( r1=0.5, r2=0.2, r=0.3, avec_tore=true )
	section = Cercle.new( r2 )           # half-circle r2 on the origine
	section.translate( [r1,0,0] )        # translation of r1
	profil = Cercle.new( 1.0 )           # unitary circle 
	pTore = Cross.new( profil, section ) # quarter of torus [0°,0°]-[180°,180°]
	pTore.rotate( [90,0,0] )             # rotated on Ox
	pTore.complet()                      # ... whole torus [-90°,90°]-[270°,270°]
	if (avec_tore)                       # display
		pTore.build( 3 )
		pTore.draw( "S" )
	end
	pCercle = Cercle.new( r )            # arc of circle 180°, radius r
	pCercle.translate( [0.5,0.5,0.0] )   # locally defined on the torus
	pCercle.complet()                    # whole circle on 360°
	tab = pCercle.build( 5 )             # table generated by subdivision
	tab.each_index do |i|
		tab[i] = pTore.get_point( tab[i] )  # transposition in global
	end
	pf = PF.new( tab )
		pf.draw( "L" )               # already subdivised before local -> global
end

many others things

on process ...