... and this page in english .
En préambule, un rappel de quelques idées :
Il y a d'un côté la géométrie classique élémentaire faite de droites et de cercles qui se peuvent dessiner avec une simple corde, des piquets et un crayon. A l'autre bout il y a la géométrie des formes courbes complexes qui ne se laissent approcher qu'à travers des formes tensorielles différentielles pleines de symboles de Christophel et autres opérateurs bien éloignés du crayon et de la corde. Je cherche une géométrie entre les deux, une géométrie construite sur un algorithme simple - l'algorithme de "de Casteljau" -, une géométrie faite de formes gauches obtenues par application récursive d'un opérateur multilinéaire. Des formes dont chaque point s'exprime comme combinaison linéaire de points à coefficients binomiaux (Pascal). Des formes qui se situent dans les tout premiers termes d'un développement en série.
Par exemple, je pense au développement en série de la chaînette [ ch(x) = 1 + x^2/2! + x^4/4! + ... ] qui conduit à la parabole si elle est limitée au second terme. Pour la conception de la Sagrada Familia, l'architecte catalan Antonio Gaudi, dans les dix dernières années de sa vie, avait abandonné ses constructions "naturelles/organiques" optimales à base de chaînettes pour revenir à de simples paraboles, non optimales mais approximations excellentes bien plus faciles à combiner, à partager et à transmettre sur un chantier.
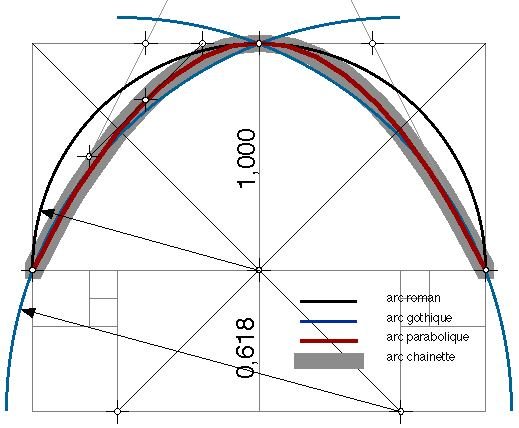
Au début était l'Architecture Romane à base de demi-cercles faciles à tracer et à combiner en voûtes et intersections mais bien loin de la chaînette courbe optimale ; c'était le premier terme de la série. Puis vint l'Architecture Gothique avec son arc brisé proche de la chaînette fait de deux arcs de cercle et préservant ainsi les techniques du passé ; c'était le deuxième terme de la série. Puis vint le jeune Gaudi qui voulait la chaînette quelle que soient les difficultés pour la tracer et la combiner, qui voulait tous les termes de la série jusqu'à l'infini, tout et tout de suite. Avec l'âge vint la sagesse et il redescendit d'un cran pour travailler avec la parabole, troisième terme de la série. Il suffit de voir le résultat, la nef de la Sagrada Familia par exemple, pour comprendre la puissance de ce renoncement.
Aujourd'hui les ordinateurs nous donnent accès à des formes a priori libres de toutes contraintes et les jeunes architectes s'en donnent à coeur joie, sautant du troisième terme à l'infini comme Gaudi l'avait fait avant eux, oubliant les leçons du passé, et faisant bien souvent n'importe quoi ! C'est ma lecture de l'évolution des formes courbes en architecture, et je propose un élément de réponse avec ce que j'appelle "Les Formes Pascaliennes", qui pourraient peut-être nous accompagner dans notre quête des termes suivants du développement en série.
alain marty
formes élémentaires

formes amorphes ?
Les pFormes élémentaires sont en fait des formes « amorphes », des formes dont les points de contrôle sont placés n'importe où dans l'espace. Pour être plus juste, ces formes ne sont pas complètement « amorphes », les points de contrôle distribuent leurs points en aussi grand nombre qu'on peut le souhaiter en des positions totalement déterminées par application récursive de simples combinaisons linéaires. Ce sont des « formes multilinéaires récursives » conduisant par réduction/diagonalisation à des formes aussi complexe qu'on le souhaite mais dont les équations sont toujours des polynomes finis. La particularité de ces polynomes est que leurs coefficients sont ceux du triangle de Pascal, dont est tiré le nom des « formes pascaliennes ». Si vous avez oublié ce qu'est le triangle de Pascal, considérez cette suite de nombres :
1 un point (pP1)
1 1 un segment (pL2)
1 2 1 une parabole (pL3)
1 3 3 1 une cubique (pL4)
1 4 6 4 1 pas de nom connu (pL5)
. . . . . . . . . . . .
Vous voyez ? Si vous avez l'esprit plus « physicien/mécanicien » que mathématicien, vous pouvez penser aux combinaisons barycentriques de masses, au centre de gravité d'un ensemble de points massiques. Tous les points de ces formes sont disposés dans une sorte d'équilibre de masses très naturel. Les fans de statistiques et de probabilités peuvent également penser aux lois de distribution, on y est en plein. Ces formes sont « naturelles », elles correspondent à de nombreux phénomènes naturels traduisant l'équilibre d'actions, de masses, d'occupation d'espace, d'optimisation. Elles sont très générales donc (voir la page coniques pour plus de précisions sur ce point).
un exemple
Voici le code la générant la première image :
def exemple()
# un tableau de points bidimensionnel :
surf = [[ [-0.5, 0.5, 0.0], [0.5, 0.5,-0.5] ],
[ [-0.5,-0.5,-0.5], [0.5,-0.5, 0.0] ] ]
pS22_0 = PF.new( surf ) # une première pSurface
pS22_0.stretch( [0.25,0.25], [0.75,0.75] ) # rétrécie
pS22_1 = PF.new( surf ) # une seconde pSurface
pS22_1.translate( [0.0,0.0,0.5] ) # déplacée
pS22_1.rotate( [0,0,-15] ) # et pivotée
pV222 = PF.new( [ pS22_0.poles(), pS22_1.poles() ] ) # un pVolume
pV222.build( 2 ) # construit
pV222.draw( "V" ) # et affiché en volume (6 faces)
pS = pV222.diag() # sa pSurface diagonale
pS.stretch( [0.25,0.25], [0.75,0.75] ) # rétrécie
pS.build( 3 ) # construite
pS.draw( "S" ) # et affichée en surface
pL = pS.diag() # sa pCourbe diagonale
pL.stretch( [-1.0], [2.0] ) # étendue
pL.build( 5 ) # construite
pL.draw( "P" ) # et affichée
end
explication
On construit un tableau de 4 points, surf, à partir duquel on construit deux facettes gauches identiques (plus connu sous le nom de PH, paraboloïde hyperbolique). La première facette est légèrement reduite dans sa surface initiale, ce n'est pas une homothétie, la seconde est translatée sur l'axe OZ et pivotée de 15° sur cet axe. Ces deux facettes sont combinées en un cube gauche pV222 qui est affiché (les 6 facettes gauches l'enveloppant). La diagonale de ce volume est une surface qui est réduite (dans sa surface initiale) et affichée. La diagonale de cette surface est une courbe, étirée (dans sa courbe initiale) et affichée sous forme d'une suite de points.
diverses choses
Une pCourbe, une pSurface, un pVolume sont tous des combinaisons linéaires barycentriques de points ; ils sont créés et traités de la même façon engendrant ainsi de nombreuses propriétés. On peut définir des hyper_pVolumes et au delà des pFormes de dimensions quelconques. Quel peut être l'intérêt de travailler avec de telles pFormes ?
- Une pForme peut être diagonalisée, engendrant une pForme de dimension inférieure mais de complexité plus grande ; par exemple la diagonale seconde d'un cube (pForme multilinéaire) est une ... cubique (définie par un polygone cubique).
- Inversement, une courbe complexe (construite sur un polygone à haut degré) peut être considérée comme la diagonale nième d'une pForme plus simple (un hyper_pVolume multilinéaire). Cette façon de faire est commune en mathématiques et souvent riche de résultats.
Les pFormes peuvent être combinées linéairement pour produire de nouvelles pFormes : par exemple la combinaison pS1 + pS2 - pS3 produit une pSurface ; et cette pSurface est une surface de Coons si les courbes limites des 3 pSurfaces sont concourantes deux à deux. On a ainsi une méthode simple pour créer une surface interpolant un contour constitué par 4 courbes.
Cette unicité permet également de traiter les déformations globales d'une pForme complexe en l'immergeant dans une pForme de dimension supérieure et de complexité inférieure : par exemple on peut immerger une pSurface dans un pCube construit sur 8 points (ou plus si nécessaire) et déformer globalement la pSurface en agissant sur les 8 points.
Les pFormes tentent de combler une « lacune » existant entre les formes simples comme le cercle, les coniques, la sphère, le tore, et les formes prises dans toute leur généralité (on peut dire amorphes) étudiées dans les cours de géométrie différentielle des universités. Dans l'approche classique, on étudie le plan tangent en un point d'une surface, puis la quadrique osculatrice, et puis c'est le grand vide ... Pour ceux qui ont entendu parler des développements en série de Taylor (ou de MacLaurin), on peut dire que les pSurfaces pS22, pS32, pS33, pS34, etc... sont les premiers termes d'un développement en série d'une forme quelconque. Et il est plus facile de manipuler une pS33 qu'une quadrique osculatrice ...
...à suivre
articles
Une approche simplifiée sur les pFormes est proposée dans un article paru en Janvier 2003 dans la revue "TANGENTE" et téléchargeable au format pdf (1,2Mo) : tangente. Un autre article est visible à la page straightaway, focalisant sur le concept de lignes droites dans les formes gauches.